The following article introduces Autoencoders that operate on images. Nevertheless, many aspects described here also apply for Autoencoders that operate different types of data.
Autoencoders are Machine-Learning models that learn to replicate data that is provided as input in the output the generate. Accordingly, Autoencoders operate as copy machines. What makes an Autoencoder’s task both challenging and interesting is the fact that it has to deal with an information bottleneck. Data that passes through this bottleneck is of much lower dimension than that of the input and output data. In order to succeed in their data replication task, Autoencoders have to learn an effective abstraction of the data. This abstracting plays the role of an encoding of the data from which it can be faithfully reconstructed.
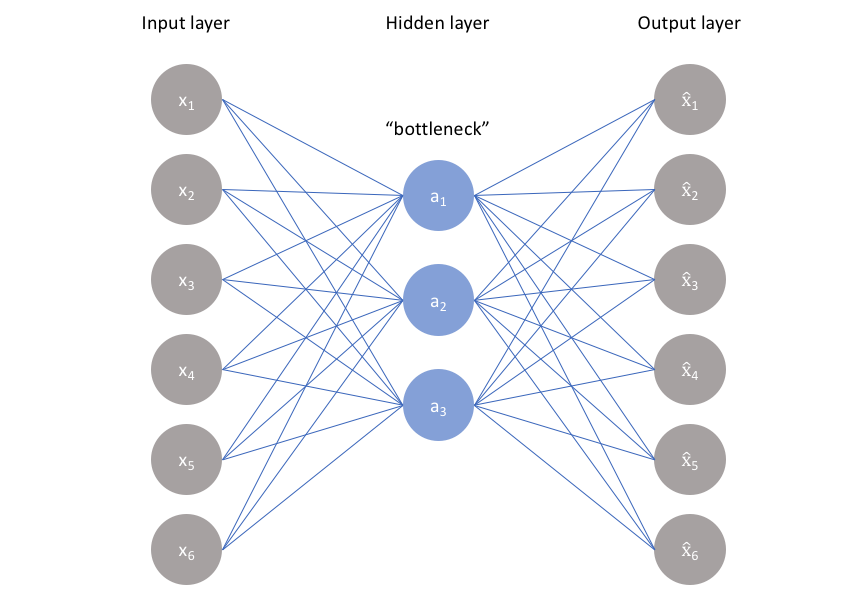
Autoencoders are the somewhat related to Generative Adversarial Networks. They are also frequently used for creating synthetic images. Autoencoders consist of two models, named Encoder and Decoder. The Decoder plays the same role as a Generator in a GAN. The Decoder takes as input a low dimensional vector and generates a synthetic image from it. Contrary to a GAN, this vector does not contain random values. Instead, it is generated by the Encoder. The Encoder takes an image from a dataset and generates a latent vector that represents the image’s encoding. This vector is then passed as input to the Decoder which generates a synthetic replica of the original image.
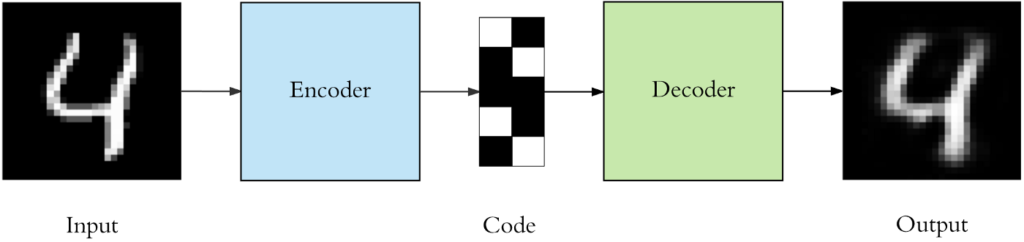
The Encoder and Decoder parts of an Autoencoder are implemented as neural networks. In the case of Autoencoders that operate on images, these networks are convolutional neural networks.
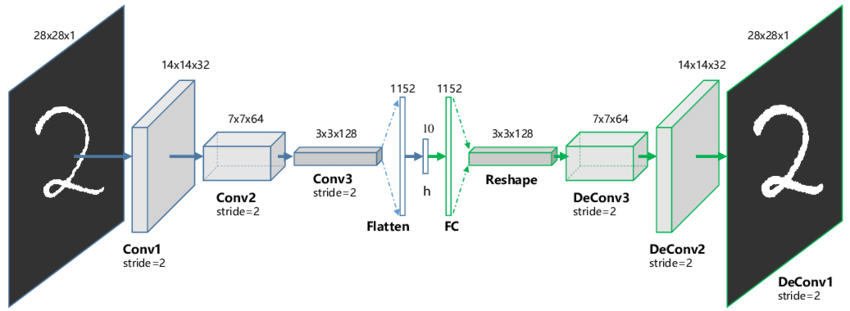
During training, the Autoencoder tries to minimise the reconstruction error between the original and synthetic image. Both the Encoder and Decoder models are trained in parallel. After training, the Encoder is usually no longer used. Instead, latent vectors are created either randomly or using vector arithmetic are then input into the Decoder to generate new synthetic images.
Latent Vector Arithmetic
One of the fascinating aspects of working with machine learning models that operate on latent codes such as GANs and Autoencoders is to explore how variations of latent codes that encode a known image might lead to the generation of interesting new synthetic images.
Vector Interpolation
One approach of creating such variations is to interpolate between two or more known encodings for images. By interpolating, new encodings are created that, once decoded, lead to synthetic images that combine some of the characteristics of the original images. This combination is not the same as a simple blending between images (which is obtained when the images themselves and not their encodings are interpolated). Instead, it is the codified abstractions used in the encodings that are interpolated and that manifest as a blending of higher level abstractions of images. This includes for example a morphing of the shape or type of the depicted objects.

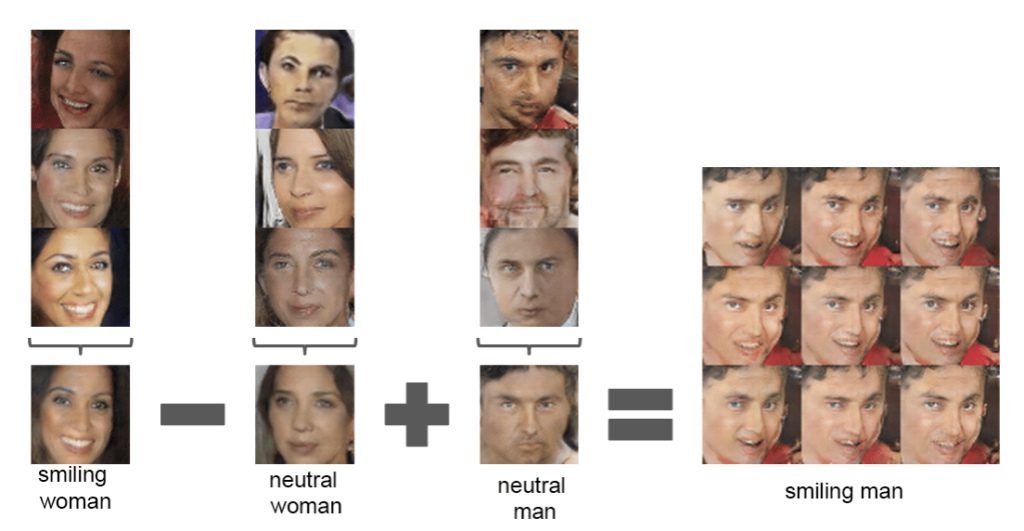
Vector Subtraction and Addition
Another approach is to conduct vector operations on encodings, such as adding or removing differences between two encodings to another encoding. Following this approach, specific properties of an image can be selectively changed. The typical method for doing this is as follows: The encodings of all the images that contain one version of the selected property (such as a smiling facial expression) are combined into one averaged encoding. The same is done for the other version of the selected property (such as a non-smiling facial expression). Then a difference encoding is calculated by subtracting the average encoding for non-smiling faces from the average encoding from smiling faces. This difference encoding, when added to any encoding of a non-smiling face, will create, once decoded, the same face but with a smiling facial expression.
Latent Space Organisation
Unfortunately, a vanilla Autoencoder such as the one described above won’t create encodings that are suitable for latent vector arithmetic. Variations of latent vectors can only be decoded into meaningful images, if the distribution of latent vectors within latent space fulfils two criteria. First, the latent space doesn’t contain any gaps. Gaps in this case are regions in latent space that don’t encode meaningful images. Second, images that are similar to each other should have their encodings lie close to each other in latent space. Then the Euclidean distance between encodings is a measure of similarity between the images they encode. If this is not the case, then a gradual interpolation between known encodings of images won’t lead to images that gradually increase and decrease the features of the original images. Instead, these features would arbitrarily change.
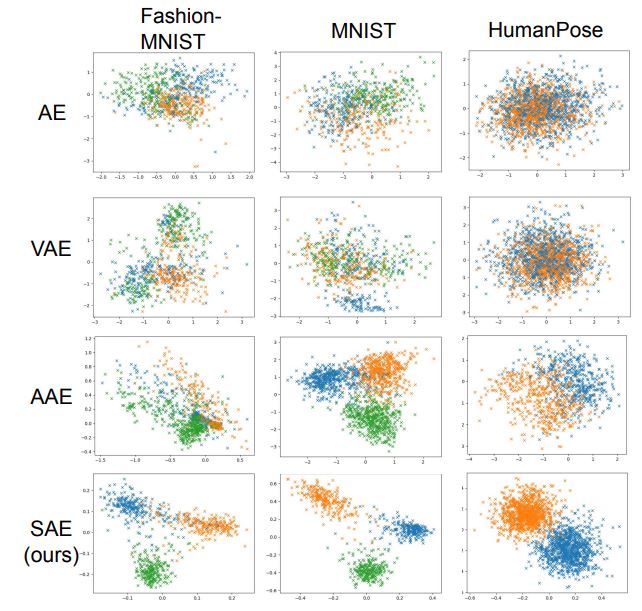
Two types of Autoencoders that have been devised to improve the organisation of latent space are briefly introduced in the remainder of this article.
Variational Autoencoder
Variational Autoencoders (VAE) differ from vanilla Autoencoders (AE) in that the former are probabilistic and the latter deterministic. In a AE, the Encoder generates from an input image a single deterministic encoding. This encoding is directly decoded by the Decoder into a synthetic image. In a VAEs, the Encoder generates from an input image the parameters for a gaussian distribution of encodings. These parameters are the mean and the standard deviation for each of the dimensions of the encoding. The Decoder then samples from this distribution to obtain an encoding that is then decoded into a synthetic image.
The error that a VAE tries to minimise is a combination of two errors, a reconstruction error (which is the same as used when training a AE) and a Kullback-Leibler divergence. In a nutshell, this divergence is large if two probability distributions don’t match, otherwise it is small.
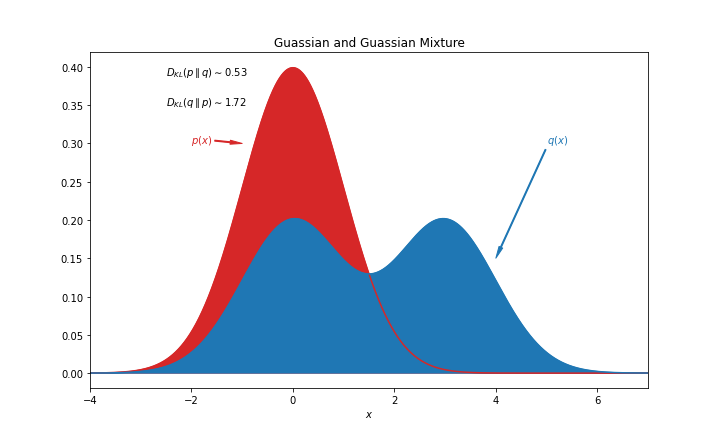
In the case of a VAE, the two distributions that should match are the distribution generated by the Encoder (the predicted distribution) and a set of Gaussian distributions whose mean is at zero and that have a standard deviation of one. Minimising the divergence causes the distributions of the encodings created by the Encoder to cluster close together while the Euclidean distance between the encodings is representative of the similarity between the encoded images. For a more in depth and mathematical explanation of VAE, the article “Variational Autoencoders – in depth explained” is a good resource.
Adversarial Autoencoder
An alternative approach to obtain a well organised latent space is to add an Discriminator model to the Autoencoder. The role of the Discriminator is similar to the role of the Critique in a Generative Adversarial Network (GAN), that is to distinguish between real and fake instances of data. For this reason, this type of Autoencoders is named Adversarial Autoencoder (AAE). In an AAE, the Discriminator’s task is to distinguish between values taken from a real Gaussian Distribution and values generated by the Encoder. Accordingly, the Discriminator is a classifier for real versus fake random variables.
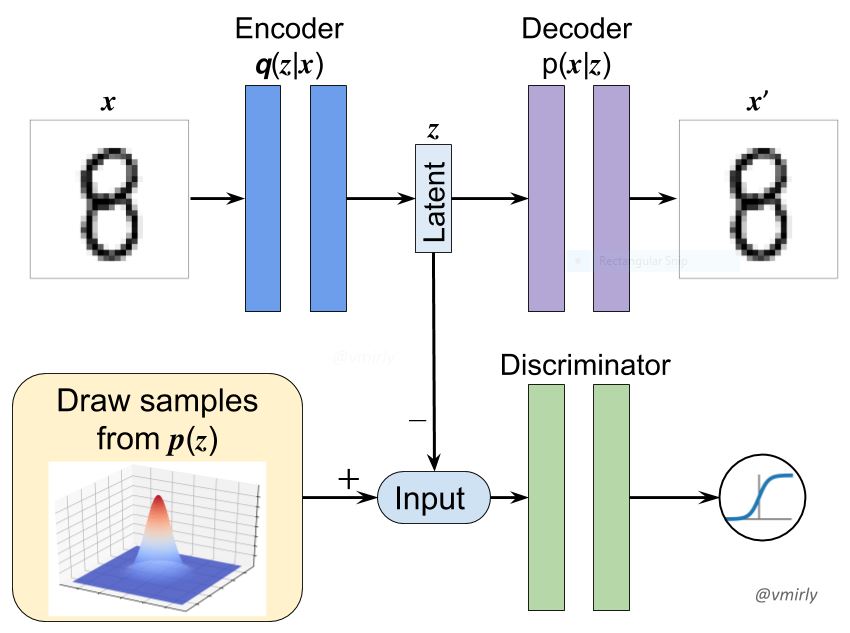
For a more in depth and mathematical explanation of AAE, the article “Adversarial Auto Encoder (AAE)” is a good resource.