Mass-Spring simulations model the behaviour of point-like objects that possess a mass and that are connected with each other by springs. Mass-points and springs can be combined into networks to model the elastic behaviour of arbitrary shapes. Mass-Spring simulations are attractive because they are easy to implement and generate rich and realistic dynamic behaviours.
Interconnected mass-points and springs are typically simulated as so called mass-spring-damper systems. These systems not only exhibit elastic behaviours but they also dissipate energy (due to friction) and eventually come to rest when they are no longer excited through external forces. Without the damping part, mass-spring systems would continue to oscillate forever.

The force exerted by a spring can be mathematically described by a simple differential equation:
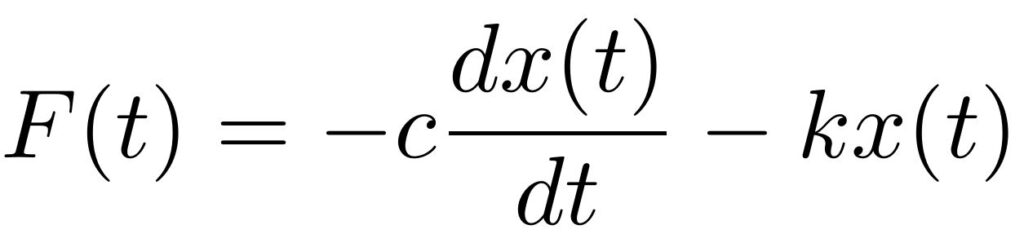
As can be seen in the above equation, the spring force points into the negative direction of the spring’s deviation from its rest length. The rest length in this simple equation is zero. The more the spring’s actual length deviates from the rest length, the larger the absolute value of the force. The stiffness represents the proportionality factor between force and deviation from rest length. The force resulting from damping points in the negative direction of the velocity of the mass-point. The faster the mass-point moves, the larger the absolute value of the force. The damping coefficient represents the proportionality factor between force and velocity.
The above equation doesn’t represent a particularly interesting mass-spring system. The spring is attached to only one mass-point that can move, has a rest length of zero, and displacement is only along the horizontal axis. A more realistic setting is represented by the next equation. Here, the spring is attached to two mass-points, the rest length is non-zero, and displacement can happen in any direction.

This article won’t go into any more detail concerning the mathematics of mass-spring damper systems. Instead, the remainder of the article deals with the simulation of elastic materials using mass-spring-damper systems. For this method, an example is given from the author’s own artistic work.
Elastic Meshes
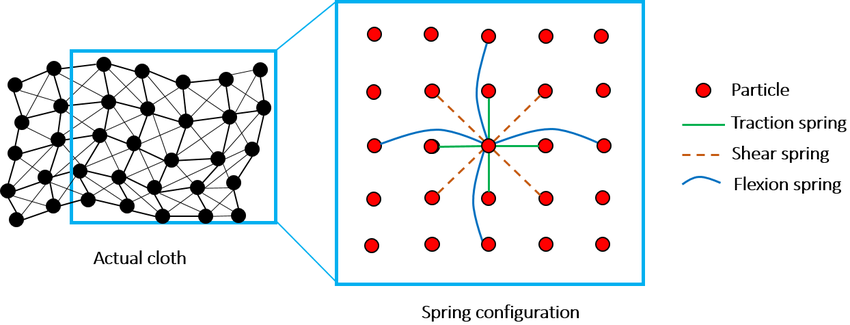
The previously described mass-spring-damper systems can be used to simulate elastic objects of arbitrary shape. This is achieved by organising the mass-points and springs in a mesh structure in which mass-points are connected to each other via multiple springs. Depending on the placement of the springs, different types of structural forces can be simulated. This is illustrated in the following figure for a two dimensional mesh that is used to simulate the mechanical properties of a piece of cloth.
Example Work: Strings
A similar approach to model an elastic surface has been used in a generative system that creates visuals that oscillate when excited by an acoustic input signal. This system forms part of an audio-visual concert entitled Strings that involves three instruments: an acoustic violin, a synthetic acoustic instrument, and a synthetic visual instrument. These three instruments are related to each other conceptually, technically, and aesthetically by sharing the same physical principle, that of a vibrating string. In case of the synthetic instruments, the vibrating strings are simulated using mass-spring-damper systems.
Contrary to the cloth simulation mentioned previously, the mass-spring system used here is not organised in a fixed regular lattice. Rather, it is repeatedly created and destroyed based on an image that either comes from a live camera or from an archive of stored images. The conversion of an image into a mass-spring system is depicted in the figure below. The conversion steps are as follows: 1. The background is removed from an image 2. the image is blurred and edges are detected 3. The edges are triangulated into multiple regions depending on the colour content of the image 4. The triangulated regions are converted into mass-spring networks. 5. The mass-spring network is rendered together with the colour content from the original image.
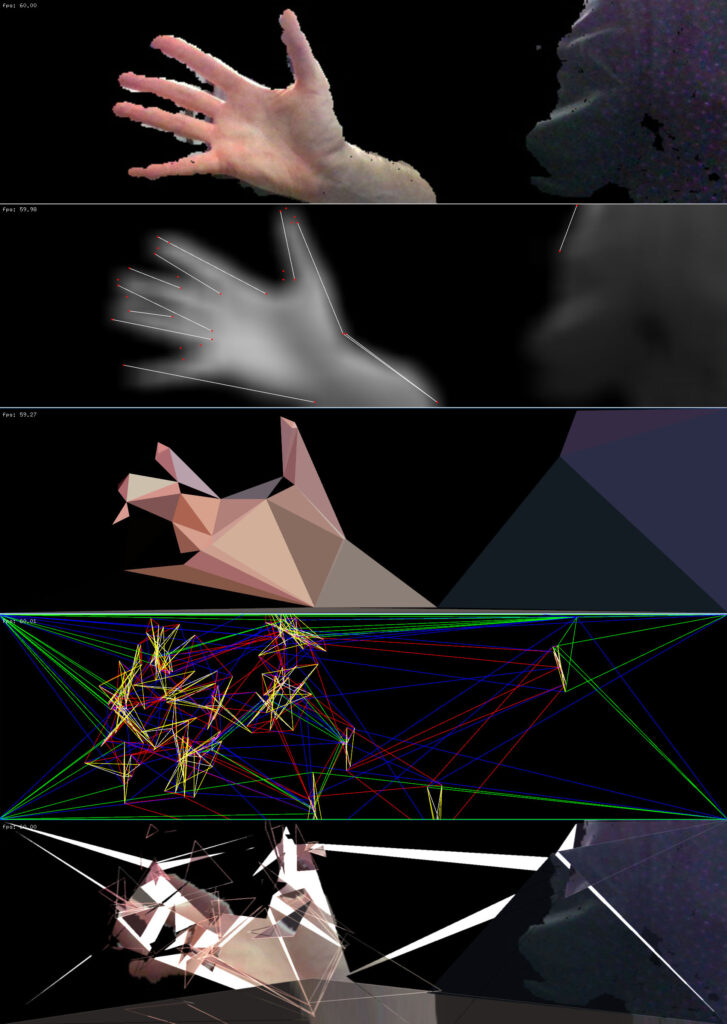
The resulting mass-spring systems are put into oscillation by periodically changing the springs’ rest-lengths. The strength of these oscillations and the selection of springs that are affected depends on a simulated acoustic resonance effect. For this, the frequency content of the acoustic output of the violin and the synthetic acoustic instrument is analysed and the most dominant spectral peaks are isolated. The frequencies of these peaks are then mapped to a range of spring lengths. Those springs that possess rest-lengths that fall within these ranges are made to oscillate by periodically changed their length at a frequency and amplitude that is proportional to those recorded in the acoustic input.